As part of my master’s project, the analytic structure of the gluon and ghost propagators was studied, together with some of the information that we can retrieve from it, particularly about confinement.
In a Quantum Field Theory, the analytic structure of the 2-points correlation functions, i.e. the propagators, enclose information about the properties of the corresponding quanta, particularly if they are or not confined. However, in Quantum Chromodynamics (QCD), we can only have an analytic solutionin a perturbative picture of the theory, which is valid for ultraviolet momenta (because of asymptotic freedom of QCD), but not in the infrared region. In order to access this specific region of the momentum space, we need to turn our attention to the non-perturbative solutions for the propagators. There, we resort to numerical solutions of QCD as, for example, those computed via Monte Carlo simulations on the lattice.
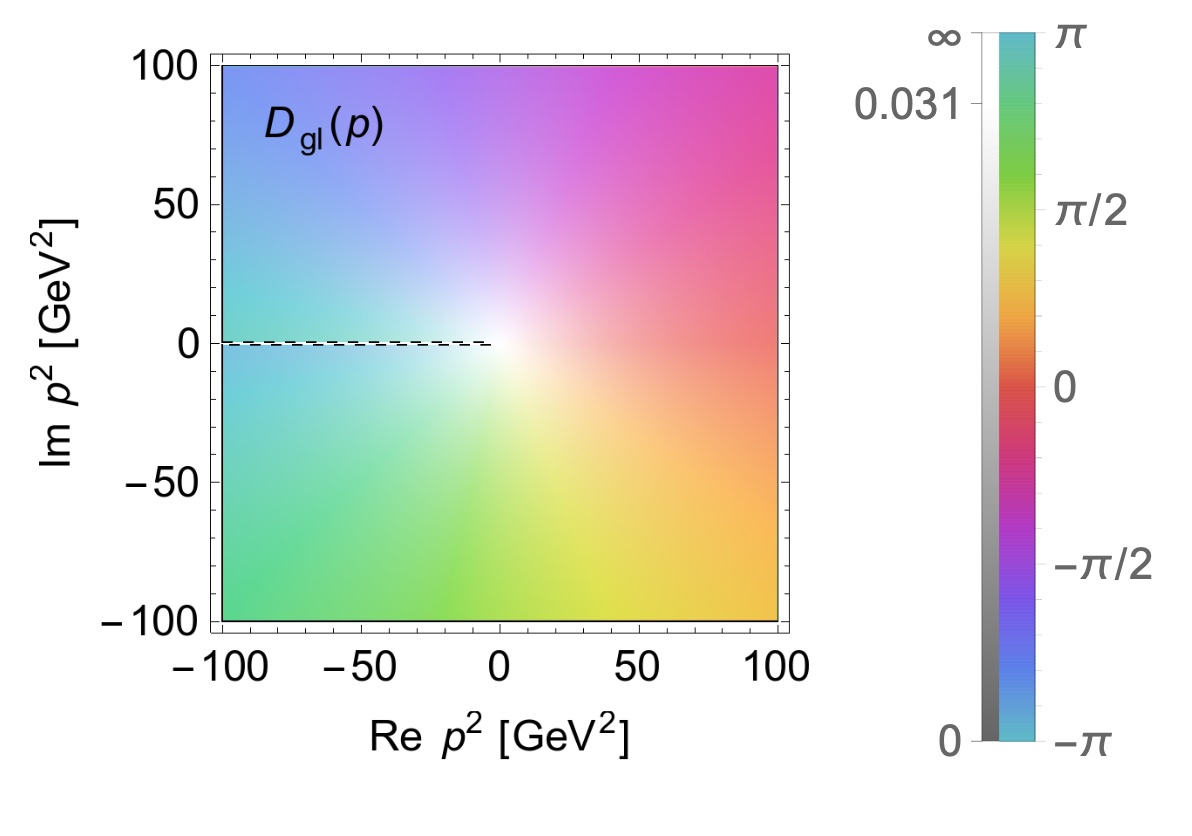
The most interesting result of this work was the identification of a conjugate pair of complex poles for the gluon propagator.
We relied on Padé Approximants (PA) to approximate the numerical data for the gluon and ghost propagators given by the Monte Carlo simulations, and investigated their analytic structures. In a first stage, we explored the advantages of using PAs when reproducing the properties of a general function, focusing on the reproduction of its analytic structure. Then, the use of PA sequences was tested, with increasing orders of approximation, on the perturbative solutions of the propagators. At this stage, a residue analysis helps in the identification of the analytic structure, since there are many poles that are artefacts of the method.
Since we were dealing with data points and not a known function, a way of approximating a PA to a discrete set of points had to be introduced, which it had to be test before finally applying it to the lattice gluon and ghost propagators.
The most interesting result of this work was the identification of a conjugate pair of complex poles for the gluon propagator, that is associated with the infrared structure of the theory. This is in line with the presence of singularities for complex momenta in theories where confinement is observed. As for the rest of the analytic structure, the branch cut that is expected from the perturbative analysis at high momenta was also seen, as well as a pole at non-zero momentum that might be related to de generation of mass scales that regularize the theory at low energies.